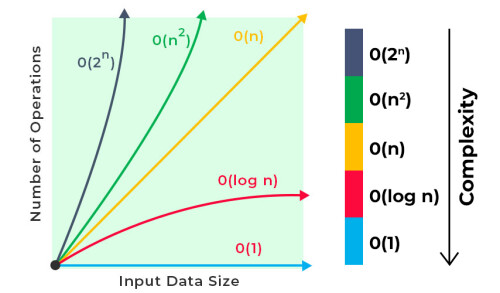
When describing the time complexity of an algorithm, we often use Big O notation to describe the growth of computation with the size of the problem. For a factorial $n!$ of positive integers, this time complexity is $O(n)$ if a general recursive implementation is used, which represents a linear increase in computational effort as $n$ grows. When $n$ is large, the computation is also considerable, and if particularly accurate results are not needed, then the approximation can be made using Sterling's formula, which reduces the time complexity to $O(\log{n})$, a very large efficiency gain.

Representation of Sterling's formula

Sterling's formula is used to find the approximation of $n!$ in the following form:

$$$ n! \sim \sqrt{2\pi n} \Big(\frac{n}{e}\Big)^n $$$

Or in the form of the expression for the limit:

$$$ \lim_{n\to \infty} \frac{\sqrt{2\pi n} n^{n} e^{-n} }{n!} = 1 $$$

The Sterling formula approximation has these 2 advantages:

1. When $n$ is small, the calculated value is already more accurate. For example, when $n = 5$, $ n! = 120$, and the approximation calculated using Sterling's formula is $118.02$, with an error of 1.6%; when $n = 10$, $ n! = 3628800$, the formula approximates $3598695.6$, with an error of 0.8%.

2. It drastically reduces the time complexity of the operation. An ordinary calculation needs to multiply from 1 to n, and the time complexity is $O(n)$, while using this approximation formula, the time complexity can be reduced to $O(\log{n})$.

The Sterling formula contains two parts of computation, squaring and computing the multiplication. For $\sqrt{n}$ the computational efficiency of squaring, using Newton's iterative method, can be considered about the same as multiplication with today's CPUs , with a time complexity of $O(M(n))$ (where $n$ indicates how many digits it has and M denotes the operational complexity of multiplication); and $n^n$ such a multiplicative computation, using recursion, it can be done with only $O(\log{n})$ time overhead - so the overall time complexity is $O(\log{n})$.

Proof of Sterling's formula

For $n!$ take the natural logarithm of:

$$$ \ln(n!) = ln(1) + ln(2) + \dots + ln(n) $$$

Since $ln $ is monotonically increasing over the domain of definition $(0, +\infty)$, we have:

$$$ \int_{n-1}^{n} ln(x) dx < ln(x) < \int_{n}^{n+1} ln(x) dx $$$

For the integers $0$ through $n$, applying this inequality above and adding them together gives:

$$$ \int_{0}^{n} ln(x) dx < ln(n!) < \int_{1}^{n+1} ln(x) dx $$$

The left end of the inequality is an improper integral, but we know it converges from the fact that its inverse function $ e^x $ is integrable (i.e., the area of the graph can be found) at $ (-\infty, 0) $. From the integral table $ \int \ln{x} = x \ln{x} - x + C$, the definite integral is found for both ends of the inequality as follows:

$$$ n \ln{n} - n < ln(n!) < (n+1) \ln{(n+1)} + 1 $$$

Next, let

$$$ d_n = \ln{(n!)} - (n + \frac{1}{2}) \ln{(n)} + n $$$

Which gives：

$$$ d_{n} - d_{n+1} = (n+\frac{1}{2}) \ln{\frac{n+1}{n}} - 1 $$$

Algebraically deform $\frac{n+1}{n}$:

$$$ \frac{n+1}{n} = \frac{1 + \frac{1}{2n+1} }{ 1 - \frac{1}{2n+1}} $$$

Based on the Taylor series (when $|x| \lt 1$):

\begin{align*} \ln{(1+x)} &= +x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \dots \\ \ln{(1-x)} &= -x - \frac{x^2}{2} - \frac{x^3}{3} - \frac{x^4}{4} - \dots \end{align*}

So:

$$$ \frac{1}{2}\ln{\frac{1+x}{1-x}} = x + \frac{x^3}{3} + \frac{x^5}{5} + \dots $$$

Since $|\frac{1}{2n+1}| \lt 1$ , we can use the above equation to obtain:

\begin{align*} d_{n} - d_{n+1} &= (2n+1)[\frac{1}{2n+1} + \frac{1}{3(2n+1)^3} + \frac{1}{(2n+1)^5} + \dots ] - 1 \\ &= \frac{1}{3}\cdot \frac{1}{(2n+1)^2} + \frac{1}{5} \cdot \frac{1}{(2n+1)^5} + \dots - 1 \\ &< \frac{1}{3} [\frac{1}{(2n+1)^2} + \frac{1}{(2n+1)^4} + \dots] \\ &= \frac{1}{3} \frac{1}{(2n+1)^2 - 1} \\ &= \frac{1}{12} (\frac{1}{n} - \frac{1}{n+1}) \end{align*}

Based on the results of the above equation, we can conclude that:

1. $\{ d_n \}$ is a decreasing sequence;

2. $\{ d_n - \frac{1}{12n} \}$ is an increasing sequence.

This means that $\{ d_n \}$ can converge to a constant $C$ and $C \gt d_1 - \frac{1}{12} = \frac{11}{12}$

$$$ \lim_{n\to \infty} d_n = C $$$

Taking the exponent for both sides of the above equation:

$$$ \lim_{n\to \infty} n! \frac{e^n}{n^n \sqrt{n}} = e^C $$$

Next it is only necessary to prove $e^C = \sqrt{2\pi}$, and here the Wallis formula previously proved is needed:

$$$ \lim_{n \to \infty} \frac{2 \cdot2 \cdot 4 \cdot 4 \cdots (2n) (2n)}{1 \cdot 3 \cdot 3 \cdot 5 \cdot 5 \cdots (2n-1) (2n+1)} = \frac{\pi}{2} $$$

To square both sides of the Wallis formula:

$$$ \frac{2 \cdot 4 \cdots (2n)}{1 \cdot 3 \cdot 5 \cdots (2n-1) \sqrt{2n}} \sim \sqrt{\frac{\pi}{2}} $$$

Multiplying the numerator and denominator on the left side by $2 \cdot 4 \cdots (2n)$, we get:

$$$ \frac{(2^n \cdot n!)^2}{(2n)!} \cdot \frac{1}{\sqrt{2n}} \sim \sqrt{\frac{\pi}{2}} $$$

Substituting $n! \sim \frac{e^c n ^ n \sqrt{n}}{e^n}$ into the above equation:

$$$ \frac{(2^n\frac{e^Cn^n\sqrt{n}}{e^n})^2}{\frac{e^C(2n)^{2n}\sqrt{2n}} {e^{2n}} } \cdot \frac{1}{\sqrt{2n}} \sim \sqrt{\frac{\pi}{2}} $$$

After simplification, we get:

$$$ e^C \sim \sqrt{2\pi} $$$

At this point, we have completed the proof of Sterling's formula.

Some mathematical conclusions used in the proof

1. Taylor expansion of $\ln{(1+x)}$

2. the calculation of $\frac{1}{x^2} + \frac{1}{x^4} + \frac{1}{x^6} + \dots $

For the first problem $f(x) = \ln{(1+x)} $, we have $f'(x) = \frac{1}{1+x}$ when $ |x| \lt 1$:

$$$ \frac{1}{1+x} = \sum_0^{\infty} (-1)^nx^n $$$

Integrating left and right simultaneously gives:

$$$ \ln{(1+x)} = \sum_0^{\infty} \frac{(-1)^nx^{n+1}}{n+1} = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \dots $$$

Replace $x$ with $ -x $ to get the expansion of $\ln{(1-x)}$.

For the second problem, which is actually the summation of the infinite geometric series:

$$$ S = a + ar + ar^2 + ar^3 + \dots $$$

Multiply both sides of the above equation by $r$:

$$$ r S = ar + ar^2 + ar^3 + ar^4 + \dots $$$

A subtraction above two equations yields:

$$$ (1-r)S = a $$$

That is:

$$$ S = \frac{a}{1-r} $$$

It is important to note that the above equation holds when $|r| \lt 1$, since it is then that its convergence is guaranteed.

In this problem $\frac{1}{x^2} + \frac{1}{x^4} + \frac{1}{x^6} + \dots $, $a = r = \frac{1}{x^2}$, so that:

$$$ S = \frac{1}{x^2 - 1} $$$